트리란?
- 트리는 계층적 구조를 가지는 자료구조로, 노드(Node)와 그 사이의 연결인 엣지(Edge)로 구성된다.
- 부모-자식 관계를 통해 노드들이 계층적으로 연결된 형태를 가진다.
- 트리는 일반적으로 계층적 데이터를 표현, 검색, 정렬과 같은 문제를 해결하는 데 사용된다.
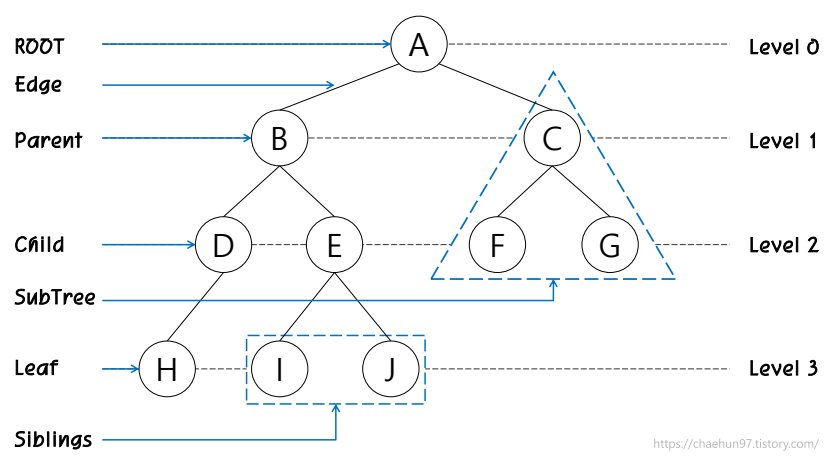
트리의 기본 구성 요소
- 노드(Node) : 트리의 기본 단위, 데이터와 자식 노드에 대한 정보를 담고 있다.(Root, Parant, Child, Leaf 등에 해당된다.)
- 엣지(Edge) : 트리의 각 노드가 부모와 자식 노드를 연결하는 선이다.
- 부모(Parent) : 자식을 가진 노드이다.
- 자식(Chlid) : 부모 노드로부터 연결된 노드이다.
- 서브트리(Subtree) : 트리의 한 노드와 그 노드의 자식들로 구성된 트리이다.
- 리프(Leaf) : 자식이 없는 노드, 트리의 끝에 위치하는 노드이다.
- 형제(Sibling) : 동일한 부모를 가지는 노드들이다.
- 깊이(Depth) : 루트 노드에서 특정 노드까지의 경로 길이를 말한다.
- 높이(Height) : 특정 노드에서 가장 깊은 리드 노드까지의 경로 길이를 말한다.
트리의 종류
일반 트리(General Tree)
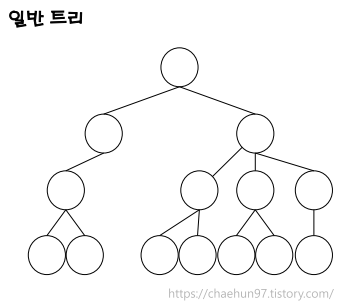
- 일반 트리(General Tree)는 부모 노드가 자식 노드를 여러 개 가질 수 있는 형태의 트리이다.
- 이진 트리(Binary Tree)처럼 자식 노드 개수에 제한이 없으며, 각 노드는 0개 이상의 자식 노드를 가질 수 있다.
이진 트리(Binary Tree)
일반 이진 트리(General Binary Tree)
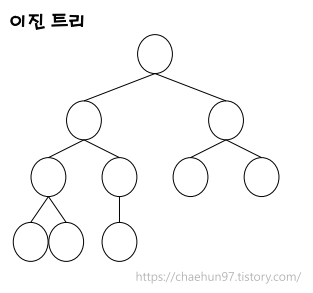
- 일반 이진 트리(General Binary Tree)는 각 노드가 최대 2개의 자식 노드를 가질 수 있는 트리이다.
- 이진 트리의 기본적인 형태로, 특정적으로 제약이 없는 일반적인 이진트리 이다.
- 왼쪽 자식(left Child), 오른쪽 자식(Right Child)로 구성되며 자식 노드가 없을 수도 있다.
편향 트리(Skew Tree)
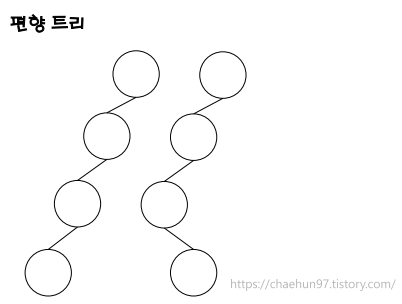
- 편향 트리(Skewed Tree)는 모든 노드가 한쪽으로만 연결된 이진 트리를 말한다.
- 트리의 높이(height)가 노드 개수(N)와 같아지는 비효율적인 구조이다.
- 일반적으로 O(log N)인 탐색, 삽입, 삭제 연산이 O(N) 으로 느려진다.
개인적인 주관으로는 편향 이진 트리는 단일 연결리스트랑 너무 비슷한것 같다.
포화 이진 트리(Full Binary Tree)와 완전 이진 트리(Complete Binary Tree)
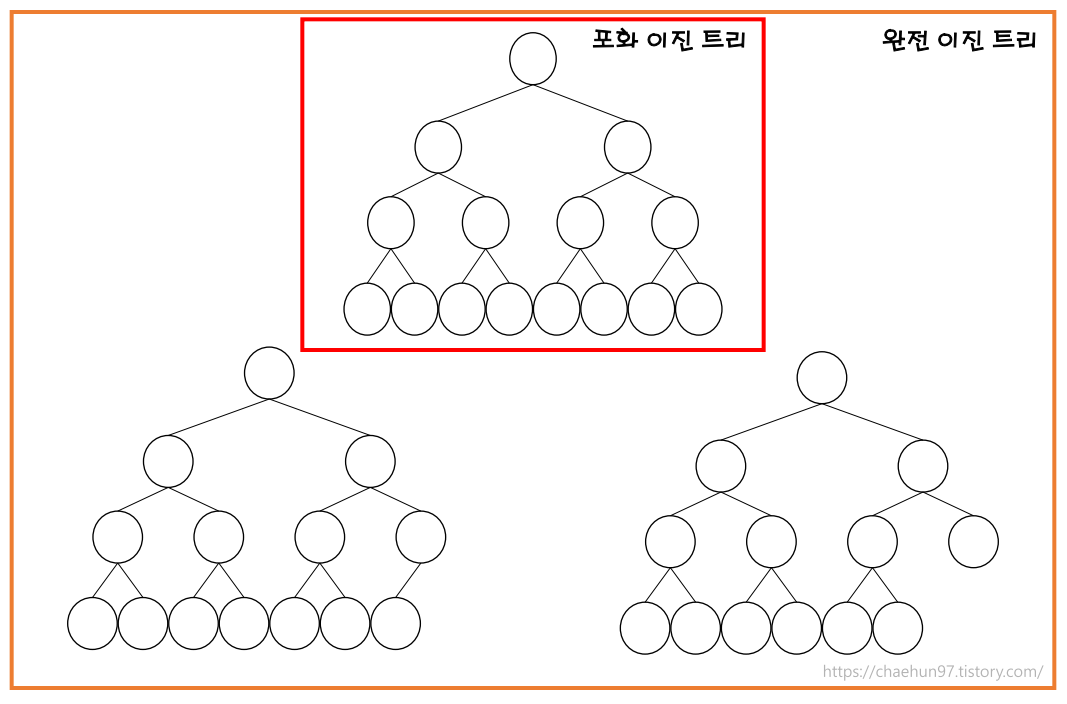
포화 이진트리(Full Binary Tree)
- 포화 이진 트리는 모든 내부 노드가 정확히 두 개의 자식을 가지며 리프 노드는 자식이 없는 트리이다.
- 모든 레벨이 꽉 차 있는 형태로 트리가 채워져야 한다. 즉, 모든 노드는 자식 노드가 0개 or 2개만 가지고 있으며 1개의 자식을 가지는 노드는 없다.
- 높이가 H인 포화 이진 트리는 노드 수가 2^h -1개이다.
완전 이진 트리(Complete Binary Tree)
- 완전 이진 트리는 모든 레벨이 꽉 차있고, 마지막 레벨만 왼쪽부터 차례대로 노드가 채워진 트리이다. 즉, 오른쪽 노드가 순서대로 없어지는 트리라고 할 수도 있다.
- 트리의 모든 노드가 위의 규칙을 따르고, 마지막 레벨은 왼쪽부터 차례대로 채워져 있어야 한다.
- 완전 이진트리는 포화 이진트리에서 오른쪽부터 하나씩 없어지는 규칙이 있는 트리이며 2^h -1 에서 2^(h+1) -1까지 될 수 있는 반면에 포화 이진 트리는 완전 이진트리의 일부라 볼 수 있으며, 모든 내부가 두 자식을 가지고 노드 수는 항상 2^h-1개인 차이가 있다.
높이가 3인 완전 이진트리와 포화 이진트리가 있다고 가정해보면
완전 이진트리르 계산해보면 2 ^ 3 -1 은 8개에서, 2 ^(3+1) - 1 = 15개가 될수 있다.포화 이진트리는 2 ^(3+1) - 1 은 15이다.
이진트리의 높이가 3이라고 가정하였을 때, 완전 이진트리는 노드의 갯수가 8개에서 15개를 가질 수 있고, 포화 이진트리는 항상 15개이다.
일반 트리 구현(JAVA)
class Node {
String data;
List<Node> children; // 자식 데이터 지정
public Node(String data){
this.data = data;
this.children = new ArrayList<>();
}
// 자식 노드 추가하기
public void addChild(Node chlid) {
children.add(chlid); // 자식을 children ArrayList에 넣는다.
}
// 현재 자식을 출력하기
public void displayChild(){
for (Node child : children){
System.out.println(child.data);
}
}
// 트리 구조 출력
public void display(int level) {
System.out.println(" ".repeat(level) + data); // 데이터를 출력
for (Node child : children) {
child.display(level + 1); // 모든 자식을 출력
}
}
}
public class GenericTree {
public static void main(String[] args) {
Node root = new Node("A");
Node b = new Node("B");
Node c = new Node("C");
Node d = new Node("D");
Node e = new Node("E");
Node f = new Node("F");
// 루트의 자식에 B 와 C를 추가
root.addChild(b);
root.addChild(c);
// 루트의 자식 출력
root.displayChild();
// B의 자식에 d와 e를 추가
b.addChild(d);
b.addChild(e);
//c의 자식에 f를 추가
c.addChild(f);
root.display(0);
}
}
일반 트리의 구조를 보면 부모 노드가 자식 노드를 여러 개 가질 수 있는 형태의 트리이다. 여러 자식들을 지정하기 위해 children 필드를 List로 선언했고, 각각의 노드에 데이터를 담기위해 data 필드를 선언했다.
멤버 메소드는 addChild, displayChild, display가 존재하는데
addchildrend은 해당하는 노드의 List에 추가하는 메소드다. child는 여러개가 될 수 있기 때문에 List를 사용하였다.
displayChild는 해당 노드의 child를 순서대로 출력한다.
display는 displayChild를 사용하며, 재귀 함수를 사용해서 child 레벨이 높아 질수록 공백을 추가하여 출력하게 했다.
이진 트리 구현(JAVA)
class BinaryNode {
int data;
TreeNode left;
TreeNode right;
public TreeNode(int data) {
this.data = data;
this.left = null;
this.right = null;
}
public void setLeft(BinaryNode left){
this.left = left;
}
public void setRight(BinaryNode right) {
this.right = right;
}
// 전위 순회 : root -> left -> right
public static void Preorder(BinaryNode treeNode){
if (treeNode != null) {
System.out.print(treeNode.data + " ");
Preorder(treeNode.left);
Preorder(treeNode.right);
}
}
// 중위 순회 : left -> Node -> right
public static void inorder(BinaryNode treeNode){
if(treeNode != null){
inorder(treeNode.left);
System.out.print(treeNode.data + " ");
inorder(treeNode.right);
}
}
// 후위 순회 : left -> right -> root
public static void Postorder(BinaryNode treeNode){
if(treeNode != null){
Postorder(treeNode.left);
Postorder(treeNode.right);
System.out.print(treeNode.data + " ");
}
}
}
public class BinaryTree {
public static void main(String[] args) {
BinaryNode treeNode1 = new BinaryNode(1);
BinaryNode treeNode2 = new BinaryNode(2);
BinaryNode treeNode3 = new BinaryNode(3);
BinaryNode treeNode4 = new BinaryNode(4);
BinaryNode treeNode5 = new BinaryNode(5);
treeNode1.setLeft(treeNode2);
treeNode1.setRight(treeNode3);
treeNode2.setLeft(treeNode4);
treeNode2.setRight(treeNode5);
System.out.print("inorder : ");
BinaryNode.inorder(treeNode1);
System.out.println("");
System.out.print("Preorder : ");
BinaryNode.Preorder(treeNode1);
System.out.println("");
System.out.print("Postorder : ");
BinaryNode.Postorder(treeNode1);
}
}
BinaryNode 클래스는 이진 트리를 구현한 클래스로, 각 노드는 data 값과 왼쪽(left), 오른쪽(right) 자식 노드를 가진다. 생성자에서 data를 설정하고, left와 right는 기본적으로 null로 초기화된다. 또한 setLeft와 setRight 메소드를 통해 각각 왼쪽과 오른쪽 자식 노드를 설정할 수 있게 하였다.
트리 순회를 위한 방법으로는 세 가지가 있는데 전위 순회, 중위 순회, 후위 순회가 있다.
전위 순회 (Preorder)
root -> left -> right 순으로 노드를 방문한다. 먼저 루트 노드를 출력하고, 그다음 왼쪽 자식과 오른쪽 자식을 재귀적으로 방문한다. 전위 순회는 먼저 루트를 처리하고, 그 후 왼쪽과 오른쪽 자식들을 처리하기 때문에, 트리의 모든 노드를 "처리"하고자 할 때 유용하다. 예를 들어, 트리의 복사본을 만들거나 트리 구조를 순차적으로 저장할 때 전위 순회가 사용된다.
중위 순회 (Inorder)
left -> root -> right 순으로 노드를 방문한다. 왼쪽 자식을 먼저 방문한 후, 루트 노드를 출력하고, 그다음 오른쪽 자식을 방문한다. 중위 순회는 이진 탐색 트리(BST)에서 매우 중요한 역할을 한다. 중위 순회는 트리를 "오름차순"으로 정렬된 순서대로 방문하므로, BST에서는 중위 순회를 통해 노드를 정렬된 순서대로 탐색할 수 있다. 예를 들어, 트리에서 값을 정렬하여 출력하거나 탐색할 때 사용다.
후위 순회 (Postorder)
left -> right -> root 순으로 노드를 방문한다. 왼쪽 자식과 오른쪽 자식을 먼저 방문하고, 마지막으로 루트 노드를 출력한다. 후위 순회는 자식들이 먼저 처리되고, 그 후에 부모 노드를 처리하는 방식이다. 이 방식은 트리 구조에서 하위 작업을 먼저 처리하고 나서 부모 노드를 처리해야 하는 상황에서 유용하다. 예를 들어, 트리 구조를 삭제하거나 트리의 자식들을 먼저 처리하고 최종적인 결정을 내려야 할 때 사용된다. 자식 노드를 모두 처리하고 나서 부모 노드를 처리하는 특성 때문에 메모리 해제와 같은 작업에도 활용된다.
위 main의 코드를 실행하면 구조는 이렇게 된다.
1
/ \
2 3
/ \
4 5
전위 순회 (Preorder)의 순서
- 1을 출력한다. -> 1 (level 1)
- 왼쪽 서브트리 2를 방문한다. (level 2)
- 2를 출력한다. -> 1 2 (level 2)
- 왼쪽 서브트리 4를 방문한다. (level 3)
- 4를 출력한다. -> 1 2 4 (level 3)
- 4의 왼쪽 자식 노드는 null. (level 4)
- 4의 오른쪽 자식 노드는 null. (level 4)
- 4의 재귀를 탈출한다. (level 3)
- 오른쪽 서브트리 5를 방문한다. (level 3)
- 5를 출력한다. -> 1 2 4 5 (level 3)
- 5의 왼쪽 자식 노드는 null. (level 4)
- 5의 오른쪽 자식 노드는 null. (level 4)
- 5의 재귀를 탈출한다. (level 3)
- 2의 재귀를 탈출한다. (level 2)
- 오른쪽 서브트리 3을 방문한다. (level 2)
- 3을 출력한다. -> 1 2 4 5 3 (level 2)
- 3의 왼쪽 자식 노드는 null. (level 3)
- 3의 오른쪽 자식 노드는 null. (level 3)
- 3의 재귀를 탈출한다. (level 2)
- 1의 재귀를 탈출한다. (level 1)
중위 순회 (Inorder)의 순서
- 왼쪽 서브트리 2를 방문한다. (level 1)
- 왼쪽 서브트리 4를 방문한다. (level 2)
- 4의 왼쪽 자식 노드는 null. (level 3)
- 4를 출력한다. -> 4 (level 3)
- 4의 오른쪽 자식 노드는 null. (level 3)
- 4의 재귀를 탈출한다. (level 3)
- 2를 출력한다. -> 4 2 (level 2)
- 오른쪽 서브트리 5를 방문한다. (level 2)
- 5의 왼쪽 자식 노드는 null. (level 3)
- 5를 출력한다. -> 4 2 5 (level 3)
- 5의 오른쪽 자식 노드는 null. (level 3)
- 5의 재귀를 탈출한다. (level 3)
- 2의 재귀를 탈출한다. (level 2)
- 1을 출력한다. -> 4 2 5 1 (level 1)
- 오른쪽 서브트리 3을 방문한다. (level 1)
- 3의 왼쪽 자식 노드는 null. (level 2)
- 3을 출력한다. -> 4 2 5 1 3 (level 2)
- 3의 오른쪽 자식 노드는 null. (level 2)
- 3의 재귀를 탈출한다. (level 2)
- 1의 재귀를 탈출한다. (level 1)
후위 순회 (Postorder)의 순서
- 왼쪽 서브트리 2를 방문한다. (level 1)
- 왼쪽 서브트리 4를 방문한다. (level 2)
- 4의 왼쪽 자식 노드는 null. (level 3)
- 4의 오른쪽 자식 노드는 null. (level 3)
- 4를 출력한다. -> 4 (level 3)
- 4의 재귀를 탈출한다. (level 3)
- 오른쪽 서브트리 5를 방문한다. (level 2)
- 5의 왼쪽 자식 노드는 null. (level 3)
- 5의 오른쪽 자식 노드는 null. (level 3)
- 5를 출력한다. -> 4 5 (level 3)
- 5의 재귀를 탈출한다. (level 3)
- 2를 출력한다. -> 4 5 2 (level 2)
- 2의 재귀를 탈출한다. (level 2)
- 오른쪽 서브트리 3을 방문한다. (level 1)
- 3의 왼쪽 자식 노드는 null. (level 2)
- 3의 오른쪽 자식 노드는 null. (level 2)
- 3을 출력한다. -> 4 5 2 3 (level 2)
- 3의 재귀를 탈출한다. (level 2)
- 1을 출력한다. -> 4 5 2 3 1 (level 1)
- 1의 재귀를 탈출한다. (level 1)
'Data Structures & Algorithms' 카테고리의 다른 글
| [자료구조] - 연결 리스트(Linked List)[1] (0) | 2024.03.20 |
|---|---|
| 배열 (Array) (1) | 2023.12.22 |
| 스택(Stack)과 큐(Queue) (0) | 2023.05.23 |
| 해시 테이블(hash table) (1) | 2023.05.06 |
| 삽입 정렬(insertion sort) (0) | 2023.05.06 |
트리란?
- 트리는 계층적 구조를 가지는 자료구조로, 노드(Node)와 그 사이의 연결인 엣지(Edge)로 구성된다.
- 부모-자식 관계를 통해 노드들이 계층적으로 연결된 형태를 가진다.
- 트리는 일반적으로 계층적 데이터를 표현, 검색, 정렬과 같은 문제를 해결하는 데 사용된다.

트리의 기본 구성 요소
- 노드(Node) : 트리의 기본 단위, 데이터와 자식 노드에 대한 정보를 담고 있다.(Root, Parant, Child, Leaf 등에 해당된다.)
- 엣지(Edge) : 트리의 각 노드가 부모와 자식 노드를 연결하는 선이다.
- 부모(Parent) : 자식을 가진 노드이다.
- 자식(Chlid) : 부모 노드로부터 연결된 노드이다.
- 서브트리(Subtree) : 트리의 한 노드와 그 노드의 자식들로 구성된 트리이다.
- 리프(Leaf) : 자식이 없는 노드, 트리의 끝에 위치하는 노드이다.
- 형제(Sibling) : 동일한 부모를 가지는 노드들이다.
- 깊이(Depth) : 루트 노드에서 특정 노드까지의 경로 길이를 말한다.
- 높이(Height) : 특정 노드에서 가장 깊은 리드 노드까지의 경로 길이를 말한다.
트리의 종류
일반 트리(General Tree)

- 일반 트리(General Tree)는 부모 노드가 자식 노드를 여러 개 가질 수 있는 형태의 트리이다.
- 이진 트리(Binary Tree)처럼 자식 노드 개수에 제한이 없으며, 각 노드는 0개 이상의 자식 노드를 가질 수 있다.
이진 트리(Binary Tree)
일반 이진 트리(General Binary Tree)

- 일반 이진 트리(General Binary Tree)는 각 노드가 최대 2개의 자식 노드를 가질 수 있는 트리이다.
- 이진 트리의 기본적인 형태로, 특정적으로 제약이 없는 일반적인 이진트리 이다.
- 왼쪽 자식(left Child), 오른쪽 자식(Right Child)로 구성되며 자식 노드가 없을 수도 있다.
편향 트리(Skew Tree)

- 편향 트리(Skewed Tree)는 모든 노드가 한쪽으로만 연결된 이진 트리를 말한다.
- 트리의 높이(height)가 노드 개수(N)와 같아지는 비효율적인 구조이다.
- 일반적으로 O(log N)인 탐색, 삽입, 삭제 연산이 O(N) 으로 느려진다.
개인적인 주관으로는 편향 이진 트리는 단일 연결리스트랑 너무 비슷한것 같다.
포화 이진 트리(Full Binary Tree)와 완전 이진 트리(Complete Binary Tree)

포화 이진트리(Full Binary Tree)
- 포화 이진 트리는 모든 내부 노드가 정확히 두 개의 자식을 가지며 리프 노드는 자식이 없는 트리이다.
- 모든 레벨이 꽉 차 있는 형태로 트리가 채워져야 한다. 즉, 모든 노드는 자식 노드가 0개 or 2개만 가지고 있으며 1개의 자식을 가지는 노드는 없다.
- 높이가 H인 포화 이진 트리는 노드 수가 2^h -1개이다.
완전 이진 트리(Complete Binary Tree)
- 완전 이진 트리는 모든 레벨이 꽉 차있고, 마지막 레벨만 왼쪽부터 차례대로 노드가 채워진 트리이다. 즉, 오른쪽 노드가 순서대로 없어지는 트리라고 할 수도 있다.
- 트리의 모든 노드가 위의 규칙을 따르고, 마지막 레벨은 왼쪽부터 차례대로 채워져 있어야 한다.
- 완전 이진트리는 포화 이진트리에서 오른쪽부터 하나씩 없어지는 규칙이 있는 트리이며 2^h -1 에서 2^(h+1) -1까지 될 수 있는 반면에 포화 이진 트리는 완전 이진트리의 일부라 볼 수 있으며, 모든 내부가 두 자식을 가지고 노드 수는 항상 2^h-1개인 차이가 있다.
높이가 3인 완전 이진트리와 포화 이진트리가 있다고 가정해보면
완전 이진트리르 계산해보면 2 ^ 3 -1 은 8개에서, 2 ^(3+1) - 1 = 15개가 될수 있다.포화 이진트리는 2 ^(3+1) - 1 은 15이다.
이진트리의 높이가 3이라고 가정하였을 때, 완전 이진트리는 노드의 갯수가 8개에서 15개를 가질 수 있고, 포화 이진트리는 항상 15개이다.
일반 트리 구현(JAVA)
class Node {
String data;
List<Node> children; // 자식 데이터 지정
public Node(String data){
this.data = data;
this.children = new ArrayList<>();
}
// 자식 노드 추가하기
public void addChild(Node chlid) {
children.add(chlid); // 자식을 children ArrayList에 넣는다.
}
// 현재 자식을 출력하기
public void displayChild(){
for (Node child : children){
System.out.println(child.data);
}
}
// 트리 구조 출력
public void display(int level) {
System.out.println(" ".repeat(level) + data); // 데이터를 출력
for (Node child : children) {
child.display(level + 1); // 모든 자식을 출력
}
}
}
public class GenericTree {
public static void main(String[] args) {
Node root = new Node("A");
Node b = new Node("B");
Node c = new Node("C");
Node d = new Node("D");
Node e = new Node("E");
Node f = new Node("F");
// 루트의 자식에 B 와 C를 추가
root.addChild(b);
root.addChild(c);
// 루트의 자식 출력
root.displayChild();
// B의 자식에 d와 e를 추가
b.addChild(d);
b.addChild(e);
//c의 자식에 f를 추가
c.addChild(f);
root.display(0);
}
}
일반 트리의 구조를 보면 부모 노드가 자식 노드를 여러 개 가질 수 있는 형태의 트리이다. 여러 자식들을 지정하기 위해 children 필드를 List로 선언했고, 각각의 노드에 데이터를 담기위해 data 필드를 선언했다.
멤버 메소드는 addChild, displayChild, display가 존재하는데
addchildrend은 해당하는 노드의 List에 추가하는 메소드다. child는 여러개가 될 수 있기 때문에 List를 사용하였다.
displayChild는 해당 노드의 child를 순서대로 출력한다.
display는 displayChild를 사용하며, 재귀 함수를 사용해서 child 레벨이 높아 질수록 공백을 추가하여 출력하게 했다.
이진 트리 구현(JAVA)
class BinaryNode {
int data;
TreeNode left;
TreeNode right;
public TreeNode(int data) {
this.data = data;
this.left = null;
this.right = null;
}
public void setLeft(BinaryNode left){
this.left = left;
}
public void setRight(BinaryNode right) {
this.right = right;
}
// 전위 순회 : root -> left -> right
public static void Preorder(BinaryNode treeNode){
if (treeNode != null) {
System.out.print(treeNode.data + " ");
Preorder(treeNode.left);
Preorder(treeNode.right);
}
}
// 중위 순회 : left -> Node -> right
public static void inorder(BinaryNode treeNode){
if(treeNode != null){
inorder(treeNode.left);
System.out.print(treeNode.data + " ");
inorder(treeNode.right);
}
}
// 후위 순회 : left -> right -> root
public static void Postorder(BinaryNode treeNode){
if(treeNode != null){
Postorder(treeNode.left);
Postorder(treeNode.right);
System.out.print(treeNode.data + " ");
}
}
}
public class BinaryTree {
public static void main(String[] args) {
BinaryNode treeNode1 = new BinaryNode(1);
BinaryNode treeNode2 = new BinaryNode(2);
BinaryNode treeNode3 = new BinaryNode(3);
BinaryNode treeNode4 = new BinaryNode(4);
BinaryNode treeNode5 = new BinaryNode(5);
treeNode1.setLeft(treeNode2);
treeNode1.setRight(treeNode3);
treeNode2.setLeft(treeNode4);
treeNode2.setRight(treeNode5);
System.out.print("inorder : ");
BinaryNode.inorder(treeNode1);
System.out.println("");
System.out.print("Preorder : ");
BinaryNode.Preorder(treeNode1);
System.out.println("");
System.out.print("Postorder : ");
BinaryNode.Postorder(treeNode1);
}
}
BinaryNode 클래스는 이진 트리를 구현한 클래스로, 각 노드는 data 값과 왼쪽(left), 오른쪽(right) 자식 노드를 가진다. 생성자에서 data를 설정하고, left와 right는 기본적으로 null로 초기화된다. 또한 setLeft와 setRight 메소드를 통해 각각 왼쪽과 오른쪽 자식 노드를 설정할 수 있게 하였다.
트리 순회를 위한 방법으로는 세 가지가 있는데 전위 순회, 중위 순회, 후위 순회가 있다.
전위 순회 (Preorder)
root -> left -> right 순으로 노드를 방문한다. 먼저 루트 노드를 출력하고, 그다음 왼쪽 자식과 오른쪽 자식을 재귀적으로 방문한다. 전위 순회는 먼저 루트를 처리하고, 그 후 왼쪽과 오른쪽 자식들을 처리하기 때문에, 트리의 모든 노드를 "처리"하고자 할 때 유용하다. 예를 들어, 트리의 복사본을 만들거나 트리 구조를 순차적으로 저장할 때 전위 순회가 사용된다.
중위 순회 (Inorder)
left -> root -> right 순으로 노드를 방문한다. 왼쪽 자식을 먼저 방문한 후, 루트 노드를 출력하고, 그다음 오른쪽 자식을 방문한다. 중위 순회는 이진 탐색 트리(BST)에서 매우 중요한 역할을 한다. 중위 순회는 트리를 "오름차순"으로 정렬된 순서대로 방문하므로, BST에서는 중위 순회를 통해 노드를 정렬된 순서대로 탐색할 수 있다. 예를 들어, 트리에서 값을 정렬하여 출력하거나 탐색할 때 사용다.
후위 순회 (Postorder)
left -> right -> root 순으로 노드를 방문한다. 왼쪽 자식과 오른쪽 자식을 먼저 방문하고, 마지막으로 루트 노드를 출력한다. 후위 순회는 자식들이 먼저 처리되고, 그 후에 부모 노드를 처리하는 방식이다. 이 방식은 트리 구조에서 하위 작업을 먼저 처리하고 나서 부모 노드를 처리해야 하는 상황에서 유용하다. 예를 들어, 트리 구조를 삭제하거나 트리의 자식들을 먼저 처리하고 최종적인 결정을 내려야 할 때 사용된다. 자식 노드를 모두 처리하고 나서 부모 노드를 처리하는 특성 때문에 메모리 해제와 같은 작업에도 활용된다.
위 main의 코드를 실행하면 구조는 이렇게 된다.
1
/ \
2 3
/ \
4 5
전위 순회 (Preorder)의 순서
- 1을 출력한다. -> 1 (level 1)
- 왼쪽 서브트리 2를 방문한다. (level 2)
- 2를 출력한다. -> 1 2 (level 2)
- 왼쪽 서브트리 4를 방문한다. (level 3)
- 4를 출력한다. -> 1 2 4 (level 3)
- 4의 왼쪽 자식 노드는 null. (level 4)
- 4의 오른쪽 자식 노드는 null. (level 4)
- 4의 재귀를 탈출한다. (level 3)
- 오른쪽 서브트리 5를 방문한다. (level 3)
- 5를 출력한다. -> 1 2 4 5 (level 3)
- 5의 왼쪽 자식 노드는 null. (level 4)
- 5의 오른쪽 자식 노드는 null. (level 4)
- 5의 재귀를 탈출한다. (level 3)
- 2의 재귀를 탈출한다. (level 2)
- 오른쪽 서브트리 3을 방문한다. (level 2)
- 3을 출력한다. -> 1 2 4 5 3 (level 2)
- 3의 왼쪽 자식 노드는 null. (level 3)
- 3의 오른쪽 자식 노드는 null. (level 3)
- 3의 재귀를 탈출한다. (level 2)
- 1의 재귀를 탈출한다. (level 1)
중위 순회 (Inorder)의 순서
- 왼쪽 서브트리 2를 방문한다. (level 1)
- 왼쪽 서브트리 4를 방문한다. (level 2)
- 4의 왼쪽 자식 노드는 null. (level 3)
- 4를 출력한다. -> 4 (level 3)
- 4의 오른쪽 자식 노드는 null. (level 3)
- 4의 재귀를 탈출한다. (level 3)
- 2를 출력한다. -> 4 2 (level 2)
- 오른쪽 서브트리 5를 방문한다. (level 2)
- 5의 왼쪽 자식 노드는 null. (level 3)
- 5를 출력한다. -> 4 2 5 (level 3)
- 5의 오른쪽 자식 노드는 null. (level 3)
- 5의 재귀를 탈출한다. (level 3)
- 2의 재귀를 탈출한다. (level 2)
- 1을 출력한다. -> 4 2 5 1 (level 1)
- 오른쪽 서브트리 3을 방문한다. (level 1)
- 3의 왼쪽 자식 노드는 null. (level 2)
- 3을 출력한다. -> 4 2 5 1 3 (level 2)
- 3의 오른쪽 자식 노드는 null. (level 2)
- 3의 재귀를 탈출한다. (level 2)
- 1의 재귀를 탈출한다. (level 1)
후위 순회 (Postorder)의 순서
- 왼쪽 서브트리 2를 방문한다. (level 1)
- 왼쪽 서브트리 4를 방문한다. (level 2)
- 4의 왼쪽 자식 노드는 null. (level 3)
- 4의 오른쪽 자식 노드는 null. (level 3)
- 4를 출력한다. -> 4 (level 3)
- 4의 재귀를 탈출한다. (level 3)
- 오른쪽 서브트리 5를 방문한다. (level 2)
- 5의 왼쪽 자식 노드는 null. (level 3)
- 5의 오른쪽 자식 노드는 null. (level 3)
- 5를 출력한다. -> 4 5 (level 3)
- 5의 재귀를 탈출한다. (level 3)
- 2를 출력한다. -> 4 5 2 (level 2)
- 2의 재귀를 탈출한다. (level 2)
- 오른쪽 서브트리 3을 방문한다. (level 1)
- 3의 왼쪽 자식 노드는 null. (level 2)
- 3의 오른쪽 자식 노드는 null. (level 2)
- 3을 출력한다. -> 4 5 2 3 (level 2)
- 3의 재귀를 탈출한다. (level 2)
- 1을 출력한다. -> 4 5 2 3 1 (level 1)
- 1의 재귀를 탈출한다. (level 1)
'Data Structures & Algorithms' 카테고리의 다른 글
| [자료구조] - 연결 리스트(Linked List)[1] (0) | 2024.03.20 |
|---|---|
| 배열 (Array) (1) | 2023.12.22 |
| 스택(Stack)과 큐(Queue) (0) | 2023.05.23 |
| 해시 테이블(hash table) (1) | 2023.05.06 |
| 삽입 정렬(insertion sort) (0) | 2023.05.06 |
