해시 테이블(hash table)
대부분의 프로그래밍 언어는 해시 테이블(hash table)이라는 자료 구조를 포함한다. 빠른 읽기라는 놀랍고 엄청난 장점이 있고, 해시, 맵, 해시 맵, 딕셔너리, 연관 배열 등의 이름을 갖는다.
다음은 해시 테이블을 사용해 파이썬으로 구현한 메뉴이다.
(파이썬에서는 딕셔너리라 부른다.)
menu = {
"one" : 1,
"two" : 2,
"three" : 3,
"four" : 4,
"five" : 5
}
쌍으로 이루어져 있으며, 첫번째 항목을 키(key)라 부르고, 두 번째 항목을 값(value)이라 부른다.
파이썬에서는 다음과 같은 문법으로 키의 값을 룩업할 수 있다.
print(menu["two"])
# 2
해시 테이블의 값 룩업은 딱 한단계만 걸리므로 평균적으로 효율성은 O(1)이다.
해시 함수로 해싱
A = 1
B = 2
C = 3
D = 4
E = 5
F = 6
#......
위 코드에 따르면,
ACE는 135
CAB는 312
DAB는 412로 변환된다.
더하기 해싱
- A + C + E = 9
- C + A + B = 6
- D + A + B = 7
- B + C + D = 9
곱하기 해싱
- A * C * E = 15
- C * A * B = 6
- D * A * B = 8
- B * C * D = 24
문자를 가져와 숫자로 변환하는 이러한 과정을 해싱(hasing)이라 부른다. 또한, 글자를 특정 숫자로 변환하는데 사용한 코드를 해시 함수(hash function)이라 부른다.
해시 함수가 유효하려면 딱 한 가지 기준을 충족해야 한다. 해시 함수는 동일한 문자열을 해시 함수에 적용할 때마다 항상 동일한 숫자로 변환해야 하며 주어진 문자에 대해 반환하는 결과가 일관되지 않으면 그 해시 함수는 유효하지 않다.
실제 쓰이는 해시 함수는 이보다 더 복잡하다. 위 예제를 통하여 해쉬 함수가 어떻게 동작하는지는 이해 할 수 있을 것이다.
조금 더 자세히 살펴보자
"곱셈" 해시 함수를 사용할 것이다.(곱셈 해시 함수로는 인덱스 0에는 아무 값도 저장되지 않으므로 제외 하겠다.)
hashT = {}

배열과 유사하게 해시 테이블은 내부적으로 데이터를 한 줄로 이뤄진 셀 묶음에 저장한다. 각 셀마다 주소가 있다.
첫 번쨰 항목을 해시 테이블에 추가해 보자.
hashT["bad"] = "evil"
# 코드로 표현하면 {"bad" : "evil"}
해시 테이블은 먼저 키에 해시 함수를 적용한다. (곱셈 해시 함수를 사용)
BAD = 2 * 1 * 4 = 8
키("bad")는 8로 해싱된다. 다음과 같이 인덱스8에 "evil"이 들어간다.

hashT["cab"] = "taxi"
# CAB = 3 * 1 * 2 = 6
# 결괏값이 6이므로 인덱스6에 저장한다.

해시 테이블 룩업
해시 테이블은 룩억하고 있는 키를 해싱 한 후 그결과가 저장된 value를 반환한다. 즉 해시 테이블에서는 각 value의 위치는 key로 결정된다. 키 자체를 해싱해 키와 연관된 값이 놓여야하는 인덱스를 계산한다.
키가 값의 위치를 결정하므로 키의 값을 찾고 싶으면 키 자체로 값을 어디서 찾을 수 있는지 알 수 있으며 키를 해싱했던 것처럼 다시 키를 해싱해 이전에 값을 넣었떤 곳을 찾을 수 있다. 따라서 왜 해시 테이블의 값 룩업이 전형적으로 O(1)인지 명확해졌다.
배열에서 항목의 값을 룩업하려면 정렬되지 않은 배열에서는 최대O(N) 정렬된 배열에서는 최대(logN)이 걸리지만 해시 테이블을 쓰면 실제 항목을 key로 사용해서 룩업을 O(1)만에 할 수 있다.
이것이 해시 테이블의 매력이라고 볼 수 있다.
단방향 룩업
해시테이블에서 한 단계만에 값을 찾는 기능은 그 값의 키를 알 때만 가능하다. 키를 모른채 값을 찾으려면 해시 테이블 내 모든 key/value 쌍을 검색해야한다. 이는 O(N)이다. 거꾸로 value를 이용해 연관된 key를 찾을 때는 해시 테이블의 빠른 룩업 기능을 활용할 수 없다. 이는 키가 값의 위치를 결정한다는 전제가 있기 때문이다.
키는 어디에 저장될까? 세부적으로 언어마다 다르지만 값 바로 옆에 키를 저장한다.
어느 경우든 해시 테이블의 단방향 속성이 갖는 다른 측면에도 주목할 가치가 있으며 각 키는 해시 테이블에 딱 하나만 존재할 수 있으나 값은 여러 인스턴스가 존재할 수 있다.
예를 들면
weight = {
"park" : 69,
"kim" : 69,
}park은 두개가 존재 할 수 없지만, 69는 중복이 될 수 있다.
해시 테이블의 문제와 충돌 해결
hastT["dab] = "pat"
# 4 * 1 * 2 = 8
# 인덱스 8에 이미 "evil"이 존재한다.

이미 채워진 셀에 데이터를 추가하는 것을 충돌(collision)이라 부른다.
충돌을 해결하는 고전적 방법중 하나가 분리 연결법(separate chaining)이다. 충돌이 일어났을때 셀에 값을 넣는 대신 배열로 참조를 넣는 방법이다.

컴퓨터는 인덱스 8에 "pat"을 추가하려 했지만 이미 "evil"이 들어 있다. 따라서 다음과 같은 배열로 대체한다.
이 배열에 포함된 하위 배열의 첫 번째 값은 단어, 두번째 단어는 그 단어의 동의어이다.
hashT["dab"] 를 룩업 할 떄는 다음과 같은 단계를 거친다.
- 키를 해싱한다. DAB = 4 * 1 * 2 = 8
- 인덱스 8을 룩업한다.
- 컴퓨터는 하나의 값이 아닌 배열들의 배열을 포함하고 있음을 알게된다.
- 각 하위 배열의 인덱스 0을 찾아보며 룩업하고 있는 단어 "dab"를 찾을 때까지 순회한다.
- 일치하는 하위 배열의 인덱스 1에 있는 값을 반환한다.
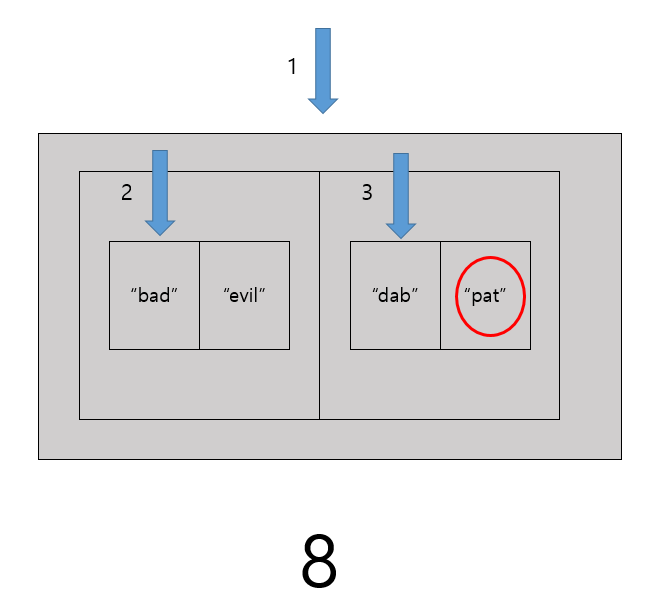
하위 배열의 인덱스 1에 있는 값인 "pat"을 찾았다.
해시 테이블이 배열을 참조할 경우 다수의 값이 들어 있는 배열을 선형 검색해야 하므로 검색에 단계가 더욱 걸린다. 만약 모든 데이터가 참조 중이라면 배열보다 나은 점이 없다. 최악의 경우 룩업 성능은 사실 O(N) 이다.
그렇기 때문에 충돌이 없도록 O(1) 시간 내에 일반적으로 룩업을 수행하도록 디자인을 해야 한다.
다행스러운 것은 대부분의 프로그래밍 언어에서 이를 대신 처리한다. 하지만 내부 동작 방식을 이해함으로써 O(1) 성능을 간신히 유지하는지 이해 할 수 있다.
효율적인 해시 테이블
해시 테이블은 세가지 요인에 따라 효율성이 정해진다.
- 얼마나 많은 데이터를 저장하는가
- 얼마나 많은 셀을 쓸 수 있는가
- 어떤 해시 함수를 사용하는가
처음 두 요인은 쉽게 이해 될 수 있지만 해시 함수 자체도 효율성을 좌우하는지 알아보자
항상 1에서 9 사이에 값만 반환하는 해시 함수를 쓰고 있다고 가정하자
- PUT = 16 + 21 + 20 = 57
- 57을 쪼갠다.
- 5 + 7 = 12
- 12를 쪼갠다.
- 1 + 2 = 3
위 해시 함수는 항상 1과 9사이에 숫자를 반환하게끔 돼 있다.

위의 해시 함수를 적용하면 10에서 16사이의 인덱스는 컴퓨터가 쓰지 않는다. 따라서 좋은 해시 함수란 사용 가능한 모든 인덱스에 데이터를 분산시키는 해시 함수이다.
충돌 조정
충돌의 횟수가 줄어들수록 효율성이 높아지지만 항목을 5개를 저장한다고 가정 하였을때 셀이 1000개면 충돌이 일어날 가능성은 거의 없으나 충돌을 피하는 것 외에 메모리를 많이 잡아먹을 것이다. 한마디로 낭비이다. 따라서 좋은 해시 테이블은 많은 메모리를 낭비하지 않으면서 균형을 유지하고 충돌을 피해야 한다.
충돌 조정을 위해 컴퓨터 과학자는 규칙을 세웠는데 데이터가 7개면 셀은10개, 14개면 20개 있어야 하는 등이다.
데이터와 셀 간의 비율을 부하율(loadfactor)라고 부른다. 이상적은 부하율은0.7이라 말할 수 있다.
만약 데이터를 추가하기 시작하면 새 데이터가 새로운 셀들에 균등하게 분산되도록 컴퓨터가 셀을 추가하고 해시 함수를 바꿔 해시 테이블을 확장할 것이다.
앞서 말했듯이 해시 테이블은 대부분 사용자가 쓰고 있는 프로그래밍 언어가 관리한다. 해쉬 함수의 종류, 해시 테이블의 확장은 프로그래미 언어가 최고의 성능을 내ㅐ도록 해시 테이블을 구현했다고 가정해도 무방하다.
해시 테이블로 간소화
해시 테이블은 쌍으로 된 데이터와 자연스럽게 들어 맞기에 조건부 로직을 간소화 가능화 할 수 있다.
일반적인 HTTP 상태 코드 번호를 반환하는 함수가 있다.
def status_doce_meaning(number):
if number == 200:
return "OK"
elif number == 301:
return "Moved Permanently"
elif number == 401:
return "Unauthorized"
elif number == 404:
return "Not Found"
elif number == 500:
return "Internal Server Error"
위 코드를 살펴 보면 상태 코드와 각각의 의미로 처리하고 있다.
해시 테이블로 조건부 로직을 완벽히 없앨 수 있다.
STATUS_CODES = {
200 : "OK",
301 : "Moved Permanently",
401 : "Unauthorized",
404 : "Not Found",
500 : "Internal Server Error"
}
der status_codemeaning(number):
return STATUS_CODES[number]
해시 테이블로 교집합 반환하기
def intersection(array1, array2):
inter = [] # 교집합이 들어갈 배열
hashTable = {} # 비교역할을 할 해시 테이블
for i in range(len(array1)):
hashTable[array1[i]] = True # 해쉬 테이블에 array1의 값들을 True로 설정한다.
for j in range(len(array2)):
if(hashTable[array2[j]]): # array2를 key로 삼아 True인 것들을 배열에 넣는다.
inter.insert(array2[j])
return inter # 교집합 반환
배열을 사용했더라면 최소 O(N2)의 성능을 가졌을 상황인데, 해시 테이블을 이용해서 O(N)까지 줄일 수 있었다.
해시 테이블은 효율적인 개발에 필수이다. O(1)의 읽기와 삽입은 쉽게 따라 잡을 수 없는 자료구조이다. 하지만 충돌, 배열참조등의 상황이 일어나면 오히려 비효율적일 수 있으며, 얼만큼의 데이터를 사용할 것과 메모리를 낭비하지 않게 부하율을 조정하는 것도 해시 테이블의 원초적인 고민도 생각 할 수 있었다. 현재는 사용하는 프로그래밍 언어들이 알아서 조정해준다니 참 고마운 일이다.
'Data Structures & Algorithms' 카테고리의 다른 글
| 배열 (Array) (1) | 2023.12.22 |
|---|---|
| 스택(Stack)과 큐(Queue) (0) | 2023.05.23 |
| 삽입 정렬(insertion sort) (0) | 2023.05.06 |
| 선택 정렬(selection sort) (0) | 2023.04.29 |
| 버블 정렬(Bubble Sort) (0) | 2023.04.29 |
